2.0. Матричное представление формул подъемной силы и лобового

аааааа сопротивления в гидравлическом приближении.

На рис. 2.1 схематически изображено взаимодействие потока с элементами самолета.

аааааааааааааааааа ааааа ааа а

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааа Рис. 2.1

На рисунке выделен условный прямоугольный параллелепипед взаимодействия потока с некоторой частью крыла, которую можно уподобить поверхности прямоугольного воздушного змея. Если разбить все крыло на такие малые части, то суммарное воздействие потока жидкости на крыло можно найти суммированием соответствующих подъемных сил и сил сопротивления. Это возможно также и в случае, если в плане крыло не представляет собой прямоугольник; достаточно знать функциональное поведениеа линий передней и задней кромки. Например, если крыло в плане представляет собой трапецию (рис. 2.2),

аааааааааааааааааа ааааааааа

ааааааааааааааааааааааааааааааааааааааааааааааа ааааааааа Рис. 2.2

то, задавая соответствующим образом уравнения прямых передней и задней кромки, мы можем рассчитать все нужные величины и учесть отклонение формы крыла от прямоугольной.

ааааа Рассмотрим возникновение сил взаимодействия потока с выбранной частью крыла самолета (рис. 2.3) на основе второго закона Ньютона (или закона передачи импульса силы). (Как мы отмечали, формулы гидравлического приближенияа являются следствием этого закона, но мы используем его в той форме, в которой он, как нам кажется, лучше подходит к матричному методу).

ааааааааааааааааааааааааааааааааааааа

ааааааааааааааааааааааааааааааааааааааааааааааа ааааааааа Рис. 2.3

Закон Ньютона запишется в данном случае в виде:

ааааааааааааааааааааааааааааааааааааааааааааааа аа ,аааааааааааааа аааааааааааааааааа (2.1)

гдеа а- сила, действующая со стороны потока жидкости (газа) на участок крыла, а- промежуток времени воздействия, аа- масса жидкости, пришедшая во взаимодействиеа с

крылом за промежуток ,а аизменение скорости потока за тот же промежуток времени.

ааааааа Характеризуя характеристики падающего потока индексом 1, а отраженного Ц индексом 2, и используя соответствующие проекции векторов на оси координат, мы можем записать:

Время взаимодействия потока с поверхностью:

аааааааааааааааааа аааааааааааааааааааааааааааа ,ааааааааааааа аааааааааааааааааа (2.2)

где а- проекция ширины крыла ана горизонтальную ось, а- величина скорости потока на дальнем расстоянии от крыла, а- длина участка крыла.

Масса, прошедшая через миделево сечение крыла за промежуток :

ааааааааааааааааааааааааааааааааааааааааааааааа , аааааааа аааааааааааааааааааааааааааа (2.3)

где а- плотность потока (т.е. количество жидкости проходящее через некоторую поверхность в единицу времени, а- плотность жидкости, а-нормальное (или поперечное, в данном случае, миделево) сечение, определяемое вертикальной проекцией ширины крыла

аааааа Итак выражение для силы принимает в случаеа положения крыла по рис. 2.4 вид:

,аа аааааааааааааааааааааааааааа (2.4)

или в матричном виде:

ааааааааааааааааааааааааааааааааааааа ,аааааааа (2.5)

где коэффициент ╜ веден как усредняющая поправка, а матрица безразмерных коэффициентов аопределяет неточность гидравлического подхода по сравнению с гидродинамическим (нетрудно видеть их связь с коэффициентами алобового сопротивления, подъемной силы иа сноса).

ааааааааа Пользуясь рис. 2.4 нетрудно записать выражения для всех скоростей в выражении (2.5):

ааааааааааааааааааааааааааааааааааааа ,ааа аааааааааааааааааа (2.6)

Таким образом, выражение для составляющих силы примет вид:

ааааааааааааааааааааааааааааааааааааа , (2.7)

или

ааааааааааааааааааааааааааааааааааааа ,аааааа (2.7Т)

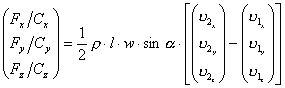аааааа Как мы видим, расчет сил оказывается существенным образом связан с углами падения и отражения потока. В общем случае, когда крыло, кроме угла поворота, т.е. угла атаки , имеет еще наклон на угола аи поворот относительно корпуса самолета на угол , составляющие скорости потока будут зависеть также от всех этих углов. Матричный метод позволяет единообразно учитывать наличие этих углов, как мы покажем ниже для более общего случая, когда плоскость имеет не только угол атаки, но и угол наклона.