ааа 2.3. Эфир как среда, поддерживающая уравненияа Максвелла

 

# [8] (стр. 352. Параграф 31). Максвелловские натяжения и тензор энергии-импульса.

Фарадей говорил о силовых линиях как об упругих трубках, переносящих натяжение и давление. Максвеллу удалосьЕ придать догадками Фарадея явную математическую форму. Так возник тензор натяжений Максвелла, релятивистским обобщением которого является тензор энергии-импульсаЕ

 

Покажем, что плотность силы Лорентца можно представить как 4-дивергенцию некоторого тензораа Е

 

# [9] Тензор энергии максвелловского поля в пустом пространстве:

Тензор содержит девять пространственных составляющих, образующих трехмерный тензор поверхностных натяжений:

аааааааааааааааааааааааааааа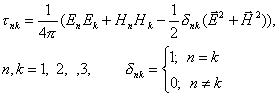

и шесть пространственно-временных компонент:

ааааааааааааааааааааааааааааааааааааа

гдеаааааааааааааааааааааааааааааааа

вектор потока энергии поля Пойнтинга и плотности электромагнитного количества движения соответственно.

Наконец временная составляющаяа является плотностью энергии электромагнитного поля:

ааааааааааааааааааааааааааааааааааааа аа

Соотношение между плотностью электромагнитного количества движения и вектором Пойнтинга является следствием симметричности тензора энергии в максвелловской теории.

В четырехмерном виде сила Лорентца записывается следующим образом:

аа ааааааааааааааа ааааааааа ,ааааа аааааааааааааааааа (1)

Подставляя из уравнений Максвелла ааи аава (1)а можно записать это выражение через напряженности поля. То же самое выражение можно получить, воспользовавшись тензором энергии-импульса электромагнитного поляа а(с учетом правила суммирования по повторяющимся индексам):

аааа аааа аааааааааааааааааааааааааааа а,ааааааааааааа (2)

(верхний индекс означает номер столбца, нижний - номер строки; по одинаковым индексам производится суммирование). #

 

В случае сплошной среды обладающей некоторыми нелинейными свойствами, эти выражения должны учитывать свойства среды. Следствием этого является введение электрической и магнитной индукций. В этом случае мы имеем.

 

# [8] (стр. 357) ааааааааааааа ааааааааа ,ааааааааааааааааааааааааааа (31.4)

где - тензора напряженностей и индукций, а L - плотность функции Лагранжа:

Тензор натяжений Максвелла , релятивистским обобщением которого является тензор энергии-импульса, входит в него следующим образом (запись условна):

ааааааааааааааааааааааааааааааа ааааа ааааааааа ,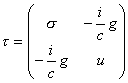

где а- тензор энергии-импульса, а- тензор натяжений Максвелла (i,j=1,2,3),

аааааааааааааааааа 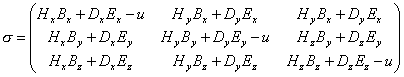,а ааааааааааа (31.10)аааааааа

- плотность энергии электромагнитного поля, а- плотность импульса электромагнитного поля.

 

Через тензор натяжений Максвелла плотность силы Лорентца выражается следующим образом:

аааааааааааааааааааааааааааааааааааааааааааааааааа аааааа ,

,

например, аааааааааааааааааааа а,аааааа ааааааааааааааа а(31.12)

где .

 

Если мы опустим здесь последний член в левой части, т.е. ограничимся для начала рассмотрением стационарного состояния, то придем к типичному условию упругого равновесия (см. "Механика деформируемых сред (8.11)). Подобно тому как напряжения, действующие в направлении x, уравновешивались объемной силойа , так и в нашем случае натяженияа аамогут полностью заменить плотность силы Лорентца. Эти натяжения полностью определены во всех точках поля с помощью тензорной схемы (31.10), в том числе и там, где по причине отсутствия зарядов нет никакой лорентцовской силы.

 

Матрицаа ааозначает в своей электрической части натяжение равноеа аав направлении силовых линий и такое же давление в перпендикулярных направлениях. Это можно сразу увидеть, если считать, например, ось x направленной вдоль ааи положить аа. Именно, мы получим тогда

аааааааааааааааааааааааааааа ааа

То же можно показать и для магнитных силовых линий, если ось x направить по силовым линиям и положитьа а. Мы возвращаемся, таким образом, к представлениям, созданным в свое время Фарадеем чисто интуитивно.

 

Поставленная в начале параграфа цель - последовательное проведение представления о перенесении силы через вакуум - тем самым достигнута.

 

Как обстоит, однако, дело в нестационарных состояниях и что означает возникающий тогда в (31.12) дополнительный член а?а Ответ на этот вопрос дает уравнение (14.1) в т.II (Механика деформируемых сред), где соответствующий член, обозначавшийся там через ааааавыражал силу инерции единицы объема упругого тела или, с противоположным знаком, изменение его импульса. Мы заключаем отсюда, что и электромагнитное поле обладает (отнесенным к единице объема) импульсом:

а ааааааааааааааааааааааааааааааааааааааааааааа ,аааааааааааааааааааааааааааааааааааааааааааа аааааааа (31.13) #

 

Формальный топологический анализ, предпринятый учеными в последние годы в области теории элементарных частиц показывает, что требование некоммутативности переменных квантовой механики (теории поля) приводит к предположению о наличии в среде вращений, которые позволяют ввести некоторые обобщенные поля и сформулировать уравнения, связывающие их, которые оказываются уравнениями Янга-Миллса.

 

Как известно, уравения Янга-Миллся являются обобщением уравнений квантовой электродинамики и, в том числе, уравнений Максвелла.

 

# [13] (стр. 128 ). Поле Янга-Миллса. аРассмотрим вращение некоторого вектора поля аав трехмерном пространствеа вокруг произвольной оси на бесконечно малый угол . Здесь величина ааесть угол вращения, а вектор азадает направление оси вращения.а Переход от начального положения вектора к конечному будет определяться преобразованием:

аааааааааааааааааааааааааааа ааа ааааа ааааааааа ,аааааааааааааааааааааааааааааааааааааа (1)

Отсюда бесконечно малое вращение запишется в виде:

аааааааааааааааааааааааааааа аааа аааа ааааааааа ,ааааааааааааааааааааааааааааааааааааа (2)

В отличие от электродинамики, где вращение происходило в одной плоскости и было коммутативно, в трехмерном пространствеа вращение в общем случае некоммутативно, что означает, что векторное произведение некоммутативно: . Это усложняет теорию,а и это усложнение имеет прямые физические следствия.

 

Будем считать, что те же самые соотношения имеют силу и в четырехмерном пространстве. Сначала отметим, что если угол асчитать постоянной величиной, то соотношение (2) представляет собой предписание произвести вращение во внутреннем пространстве переменной ана один и тот же угол аво всех точках пространства-времени. Мы можем предположить, что такое жесткое требование имеет место только в особых случаях. Если считать расстояния достаточно большими, то теория близкодействия не согласуется с таким требованием. Таким образом, следует считать, что

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ,ааааааааааааааааааааааааааааааааа ааааааааа (3)

Тогда мы будем иметь:

аааааааааааааааааааааааааааа аа аааааа ,

или

аааааааааааааааааааааааааааа а ааааааа ,ааааааа ааааааааа (4)

Другими словами, величина ане преобразуется ковариантно, т.е.а так же, как . Чтобы добиться этого, мы должны построить ковариантную производную , подобную ковариантной производной в квантовой электродинамике.

 

Оказывается, что если ввести калибровочный потенциал (т.е. компенсирующее поле)а атак, чтобы он преобразовывался по формуле:

аааааааааааааааааааааааааааа ааааааааа ,

или

аааааааааааааааааааааааааааа ааааааааа ,аааааааааааааааааааааааааааааааааааааааааааа (5)

то ковариантная производная вектора азапишется в виде:

аааааааааааааааааааааааааааа ааааааааа ,ааааааааааааааааааааааааааааааааааааааааааааа (6)

 

Далее по аналогии с тензором напряженности электромагнитного поля вводится тензор , удовлетворяющий такому же преобразованию, как и само поле :

аааааааааааааааааааааааааааа ааааааааа ,

а именно:

аааааааааааааааааааааааааааа ааааааааа ,аааааааааааааааааааааааааааааааа (7)аааа

Напряженность поля аесть вектор, а потому произведение аесть скаляр и может войти в лагранжиан, как и в случае электродинамики:

аааааааааааааааааааааааааааа ааааааааа ,аааааааааааааааааааааааааааа (8)

Уравнение движения выводятся из этого лагранжиана как обычно:

аааааааааааааааааааааааааааа ,аааааааааааааааааааааааааааааааааааааааааааааа (9)

Это уравнение аналогичноа паре уравнений Максвелла для 4-тока.

Аналогом другой пары уравнений Максвелла является уравнение:

аааааааааааааааааааааааааааа ааааааааа ,аааааааааааааааааааааааааааааааааааа (10) #

 

(Далее)

 

(Литература)

 

(В начало)